Optical Basics: What is FOV (Field of View)

Field of View (FOV ) is an important factor needed to be taken into consideration when you buy or design an optical imaging device or component. FOV describes the maximum scope at which an optical instrument could capture visible lights or electromagnetic radiations in the case of infrared thermal imaging. Field of View is measured in terms of the sensor size which forms the image and the focal length of an optical imaging device. Therefore, for beginners, before we start to discuss the field of view, we have to understand focal length first. Incidentally, if you are interested, you can also learn more in our other Optical Basics Series, which is still progressing and might update in the future. If you like these small pieces, you could continue to follow our updates:

• Spherical Aberrations and Coma
• Chromatic Distortion, Field Curvature, Distortion, and Astigmatism
• Optical Basics: The Nature of Light and Optical Elements
  

Focal length is a measurement of the extent to which the light converges or diverges in an optical system. For a Biconvex lens, Focal length is defined as the distance from the optical center and the point where lights parallel to the optical axis converge (the focal point). In more practical terms, given that the object is at an infinite distance away from the optical lenses, the focal length is the distance between the sensor/detector and the optical center of a lens module (This, however, is only an approximate measure, since in real life object at an infinite distance away is only a theoretical concept that does not exist, lights emitted from the objects, entering the lenses, could never be genuinely parallel, but always incident at a certain angle to the optical axis. Therefore, to obtain the most lucid image, the distance between the sensor and the optical center of the lens module will scarcely be identical to the focal length, but rather varied to a minute degree.)

Now assume, for the sake of the argument, there is an object at an infinite distance from a Biconvex lens, hence the image is formed at the sensor which is one focal length from the lenses. The focal length is f, and the vertical length of the sensor is h.

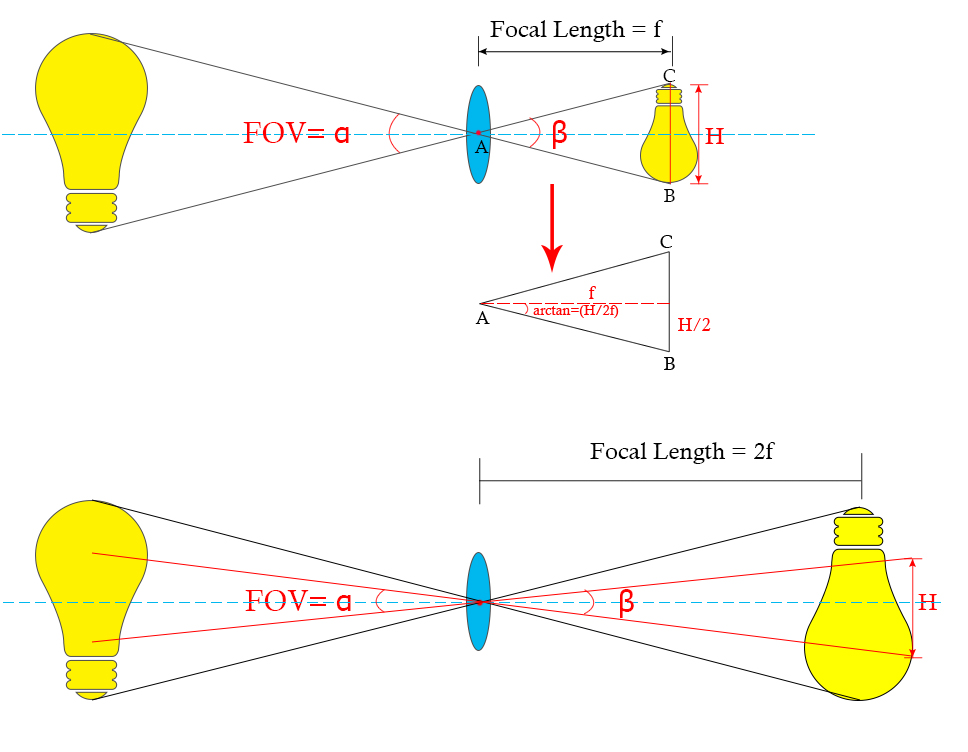
Figure 1: The fields of view of convex lenses with different focal lengths

As shown in figure 1, FOV, as an angular parameter measured in degrees, is labeled as angle α, and we could see that angle α equals to angle β according to the law of vertical opposite angles. And the value of beta could be solved using the trigonometric functions of the triangle ABC.

Therefore we get the equation:

FOV=β= 2tan^-1 (H/2f)

In comparison, there is also a convex lens with a focal length of 2f, given that the sensor size is the same, now the FOV of this imaging device is:

FOV=β= 2tan^-1 (H/2(2f))=2tan^-1 (H/4f)

Definitely, the FOV of the second configuration is narrower than the first one. This leads to the conclusion:

Given the sensor sizes same, the longer the focal length, the narrower the FOV;

The shorter the focal length, the wider the FOV.

It is also perceptible from the figures and equations above that a larger sensor will also produce a wider field of view and vice versa.

Now consider objects at finite distances from the lenses. We use the term Working Distance (WD), the interval between the lens front and the object.

Oftentimes, instead of an angular measurement of FOV, there are also circumstances that require a certain viewing scope in terms of distances. For, example, a client purchasing thermal lenses for monitoring production would expect the camera could capture the whole scene of the specific workshop or a certain machine, and it is more tangible to use measurements of length rather than angle. 

Figure 3: How to determine the FOV when you know the certain lengths you need to capture

As shown in figure 3, the 1/2 of the accessible length that an optical instrument, with a given angular FOV, is able to capture, could be seen as the base of the triangle with a vertex angle equal to 2/FOV, and the height of approximation equal to the distance from the object to the mechanical front the lenses, which is the Working Distance (WD). 

The equation could be stated as:

Accessible Length=2WD tan(FOV/2)

When you are selecting optical lenses or cameras, these equations about the calculation of FOV and its accessible length could be helpful. You might ascertain the FOV or the length first according to your requirements, and then estimate the focal length, and the sensor size using the equations. Also, you could adjust the FOV of the lenses via changing the focal length, the sensor size, and the working distance. For zoom lenses, the observer could obtain variable fields of view, zooming the lenses and continuous changing the focal length of the lens assemblies. For dual FOV lenses, there is a double focal length resulting in double FOV. These lens modules with variable focal lengths have the advantage of changing the field of view without the location-shifting of the observer, this is of extreme usefulness in the case of LWIR lenses and MWIR lenses, as thermal cameras operating at the aforesaid wavebands are often applied for warfare. For Fixed Focal Length (Prime Lenses), since the focal length is constant, one needs to change the working distance to procure a different FOV, moving toward or away from the target object.

However, it is worth noting that the equation for accessible length is not accurate, since it was a rare occasion that the entrance pupil (which is precisely the point at which the vertex of our triangle model in the equation should locate.) is positioned at the mechanical front of the lenses.  And the equation becomes invalid for applications with short working distances because the portion of deviation has increased. This is the reason for the fact that computer simulation data are utilized when it comes to the actual designing and planning of the lens architecture.

Horizontal FOV, Vertical FOV, and Diagonal FOV:

So far the calculation we have done above is about the horizontal FOV, however, often FOV should be considered in 3-dimension. Vertical FOV could be calculated given the Aspect Ratio of the senor, expressed in the equation below.

Aspect Ratio= horizontal length (width) of the detector : vertical length (height) of the detector

Therefore, conversion between the horizontal FOV, vertical FOV, and diagonal FOV could be deducted using the trigonometric functions:

vertical FOV (angular) = 2tan^-1 (height of detector/2f), and since width of detector = height x aspect ratio 

horizontal FOV (angular) = 2tan^-1 (height x aspect ratio/2f)

And if the FOV is measured as a certain length:

horizontal FOV (length) = vertical FOV x aspect ratio

Diagonal FOV measured in length unit could be seen as the hypotenuse of a right triangle with two sides equal to the horizontal FOV and the vertical FOV, hence:

diagonal FOV (length) = sqrt (vertical FOV ^2 + horizontal FOV ^2)

Tags: What is FOV (Field of View)

---