What is Second Harmonic Generation (SHG)

Abstract :

The application of Second Harmonic Generation (SHG) technique is boosting currently. If you wish to better understand the whole matter about harmonic generation, there is also a technical short piece What is Harmonic Generation in series with this one, you might want to read it. The technique has been utilized extensively as a measure to obtain laser light with short wavelengths which are not directly procurable, for example, 532nm green output for Nd:YAG lasers, or ultra-violet lights with further SHG. Understanding the concept and building up theoretical models of second harmonic generation is fundamental, whether you are an engineer designing your own lasers or looking for the crystal for SHG applications that suit your requirements best.

Second Harmonic Generation (SHG), or equivalently called Frequency Doubling is a kind of x^2 nonlinear optical effect (optical nonlinearity: the phenomenon that occurs when a strong excitation light field interacts with a certain medium, the electric polarization vector (P) of medium is no longer linearly proportionate to the excitation light field strength(E)).

SHG is one kind of optical nonlinear phenomenon and is essentially the process of halving the input wavelength (and therefore the output frequency will be twice the magnitude of the original) after delivering the light through a special media while preserving the coherence of excitation.  

Certain conditions should be met for efficient second-harmonic generation. The first is that the medium should not have an inversion-symmetric structure. Under the circumstance of electric dipole contribution, for such a media, second harmonic generation could never happen since its second-order electric susceptibility is zero.

The second is phase matching. Second Harmonic Generation is a phase-sensitive process. Phase matching directly determines the efficiencies of nonlinear optical mechanisms. If the phase-matching conditions are met, the second harmonic light waves generated at different locations in the nonlinear crystal will cumulate coherently until emerging at the exit face of the crystal （i.e. maintaining a proper relationship between the interacting waves along a propagation direction). For a second harmonic generation, mainly birefringent phase-matching techniques are utilized,   and there are four kinds of birefringent phase-matching, including critical phase matching, and non-critical phase matching. Besides birefringent phase-matching, there is also quasi-phase-matching.

Calculations and Further Understanding of Second Harmonic Generation：

Materials will be polarized under the effect of light excitation, the equation could be given:

D＝ε₀E＋P= εE

Where P is the polarization vector, E is the strength of the excitation light field, and ε₀ is the dielectric constant and magnetic conductivity of the vacuum.

For linear materials, the electric polarization vector could be written as the equation below:

P(t)=ε₀X¹E(t)

For nonlinear materials, we could perform tailor expansion to the polarization vector:

P(t)=ε₀[X¹E(t)+X²E²(t)+X³E³(t)+......] =P^linear + P^nonlinear

Where X² and X³ are the second-order electric susceptibility and the third-order electric susceptibility respectively. Naturally, the electric polarization induced from light excitation is linear, the polarization of higher orders does exist but is too feeble to capture. But for some materials, the high-order polarization is just too obvious to be ignored. Nonlinear Crystals are such materials with strong non-linear polarization.

Imagine a monochromatic planar wave with a frequency ω₁ passing through a Nonlinear SHG Crystal with a length L, obtaining an output wave with a frequency of ω₂=2ω₁ (presume there is no absorption of light in the crystal and light propagates along the z-axis).

We could summarize the electric field vector using the following equations:

E₁(z,t) = E(ω₁ )^e-iω1t + c.c = e₁A₁(z)^eik1r-ω1t + c.c
E₂(z,t) = E(ω₂ )^e-iω2t + c.c = e₂A₂(z)^eik2r-ω2t + c.c

Where Kn is the magnitude of the vector, A_n(z) is the amplitude of the electric field, and e_n is the unit vector of the polarization direction which is orthogonal to the propagation direction. The

Hence the wave equation could be written as:

▽² E_n (z,t) - n²θ²E/c²θt² = 1/ε₀ c^2 * θ²P^nonlinear/θ t²

Phase-matching:

As could be deduced from above, the relationship between nonlinear polarization strength and the electric field is:

P^nonlinear (ω₂) ∝ E(ω₁) E(ω₁)exp(-i(k₂-k₁-k₁)z)

Where k₁ is the wavenumber of the fundamental beam and k₂ is the wavenumber of the second-harmonic beam. If k₂=2k₁, there is no phase mismatch (phase mismatch therefore could be defined as Δk=k₂-2k₁, and Δk≠0 indicates the existence of phase mismatch).

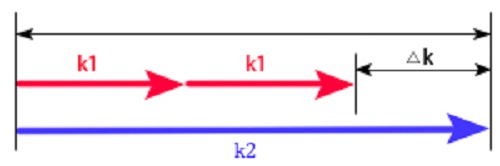
Figure 1: This is a diagram of sketch to show the relationship between k1, the wave number of the fundamental signal, and k2, the wavenumber of the frequency-doubled output signal. The lag between them △k represents the phase mismatch.

In practical circumstances, due to chromatic dispersion, the shorter the wavelength, the higher the velocity. This implies the velocity of the shg light will always be lower than the velocity of the fundamental wave, which subsequently results in a non-zero Δk.

When Δk≠0, the amplitude of the nonlinear-polarized signals will oscillate periodically in response to changes in the propagation distance, and the oscillation period is 2π/k. only when perfect phase matching is achieved, sinc²(ΔkL/2)=1, which means the intensity of the second-harmonic light is always the n-square of the length of media, obtaining maximum shg efficiencies. If there is a phase mismatch, the shg lights excited from the shg-polarized signals at different times could be interfering with each other and canceling out the shg-effect.

The Applications of Second Harmonic Generation :

Below are some prevalent Nonlinear Crystals used for second harmonic generations and their applications.

1. Beta Barium Borate (BBO), LBO, and other Borate (e.g BIBO) Crystals:

These crystals are the most eminent nonlinear optical crystals, featuring large SHG coefficients, and are excellent for second harmonic generations to produce visible and ultra-violet light output.  E.g.  BBO for intracavity SHG of Nd:YAG for 532nm output and SHG of Dye laser/Argon doped laser to deliver UV output.

It is worth noting that the nonlinear coefficient of BIBO is 3.5-4 times higher than that of LBO, and 1.5-2 times higher than that of BBO, and proved to be a promising SHG media to generate blue laser output. Furthermore, LBO crystals has the forte of realizing non-critical phase-matching (NCPM) second-harmonic generation.

2. Potassium Dideuterium Phosphate (DKDP, or KD*P) Crystals:

These crystals are an exemplary class of crystals that produce shg effects and are useful in the near-ultraviolet, visible, and near-infrared regions. The crystals feature great homogeneity, high damage thresholds but relatively low nonlinearilities. Large dimension crystals could be grown at low prices. One of its conventional shg applications is for Nd:YAG lasers at room temperature.

3. KTP, and HGTR KTP, KTA, and RTP crystals

The “KTA class” in general has large nonlinearities and capabilities for periodical poling.

KTP crystals are The best media for the SHG of solid-state green lasers, which are currently becoming favored as pumping sources and amplifiers for visible dye lasers and tunable Ti: Sapphire lasers. Flux-grown KTP crystals are cheaper, While HGTR KTP crystals grown from unique modified fluxes and heat treatment exhibits higher gray track resistance (photo darkening).

KTA crystals are superior for SHG@1.083μm-3.789μm and exhibit a higher damage threshold and lower absorption in the 3-4μm wavelength range than KTP.

4. Lithium niobate (LN), alpha lithium iodate (LiIO3) crystals, etc.

Lithium Niobate (LiNbO3) Crystals are an excellent NLO medium for SHG at wavelengths in infrared regions, with an OH- absorption at 2.87 µm. And since their refractive index is sensitive to temperature, it is possible to achieve non-critical phase-matching.
LilO3 is extensively applied for the SHG of the low and medium power Ti:Sapphire, Alexandrite, Cr:LiSrAlF6, Cr:LiCaAlF6 lasers and Nd:YAG lasers.

5. ZGP crystals

Zinc germanium phosphide is a promising mid-IR crystals and is requisite for SHG of CO2 lasers.

Related Articles

Tags: What is Second Harmonic Generation (SHG)

---